CONSTRUCTING QUANTUM ANGULAR MOMENTUM L3 IN SPECIFIC DIRECTION BY USING U(1) GROUP
Main Article Content
Abstract
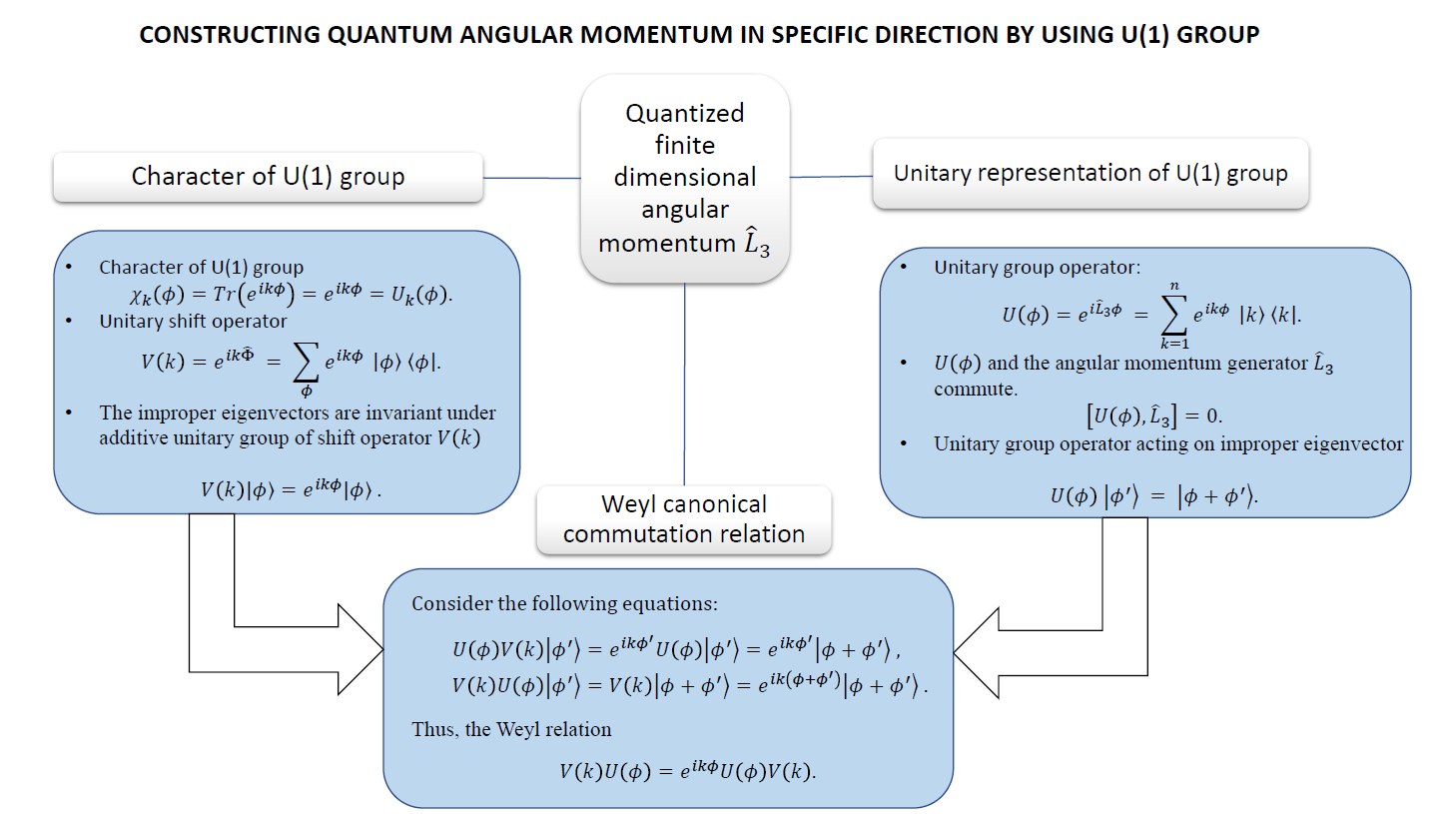
The purpose of this work is to investigate the mathematical structure of finite quantum angular momentum in a specific direction L3 which can be constructed from the representation of the U(1) group. The angular momentum eigenstate is invariant under Abelian rotation symmetry. The character group of U(1) is constructed to show that there exists an additive unitary operator for the angular momentum eigenstate, and the rotation eigenstate is invariant under it. The Weyl relation is proved by showing that the angle and angular momentum L3 are the canonical conjugate pair of observables.
Downloads
Article Details
Transfer of Copyrights
- In the event of publication of the manuscript entitled [INSERT MANUSCRIPT TITLE AND REF NO.] in the Malaysian Journal of Science, I hereby transfer copyrights of the manuscript title, abstract and contents to the Malaysian Journal of Science and the Faculty of Science, University of Malaya (as the publisher) for the full legal term of copyright and any renewals thereof throughout the world in any format, and any media for communication.
Conditions of Publication
- I hereby state that this manuscript to be published is an original work, unpublished in any form prior and I have obtained the necessary permission for the reproduction (or am the owner) of any images, illustrations, tables, charts, figures, maps, photographs and other visual materials of whom the copyrights is owned by a third party.
- This manuscript contains no statements that are contradictory to the relevant local and international laws or that infringes on the rights of others.
- I agree to indemnify the Malaysian Journal of Science and the Faculty of Science, University of Malaya (as the publisher) in the event of any claims that arise in regards to the above conditions and assume full liability on the published manuscript.
Reviewer’s Responsibilities
- Reviewers must treat the manuscripts received for reviewing process as confidential. It must not be shown or discussed with others without the authorization from the editor of MJS.
- Reviewers assigned must not have conflicts of interest with respect to the original work, the authors of the article or the research funding.
- Reviewers should judge or evaluate the manuscripts objective as possible. The feedback from the reviewers should be express clearly with supporting arguments.
- If the assigned reviewer considers themselves not able to complete the review of the manuscript, they must communicate with the editor, so that the manuscript could be sent to another suitable reviewer.
Copyright: Rights of the Author(s)
- Effective 2007, it will become the policy of the Malaysian Journal of Science (published by the Faculty of Science, University of Malaya) to obtain copyrights of all manuscripts published. This is to facilitate:
- Protection against copyright infringement of the manuscript through copyright breaches or piracy.
- Timely handling of reproduction requests from authorized third parties that are addressed directly to the Faculty of Science, University of Malaya.
- As the author, you may publish the fore-mentioned manuscript, whole or any part thereof, provided acknowledgement regarding copyright notice and reference to first publication in the Malaysian Journal of Science and Faculty of Science, University of Malaya (as the publishers) are given. You may produce copies of your manuscript, whole or any part thereof, for teaching purposes or to be provided, on individual basis, to fellow researchers.
- You may include the fore-mentioned manuscript, whole or any part thereof, electronically on a secure network at your affiliated institution, provided acknowledgement regarding copyright notice and reference to first publication in the Malaysian Journal of Science and Faculty of Science, University of Malaya (as the publishers) are given.
- You may include the fore-mentioned manuscript, whole or any part thereof, on the World Wide Web, provided acknowledgement regarding copyright notice and reference to first publication in the Malaysian Journal of Science and Faculty of Science, University of Malaya (as the publishers) are given.
- In the event that your manuscript, whole or any part thereof, has been requested to be reproduced, for any purpose or in any form approved by the Malaysian Journal of Science and Faculty of Science, University of Malaya (as the publishers), you will be informed. It is requested that any changes to your contact details (especially e-mail addresses) are made known.
Copyright: Role and responsibility of the Author(s)
- In the event of the manuscript to be published in the Malaysian Journal of Science contains materials copyrighted to others prior, it is the responsibility of current author(s) to obtain written permission from the copyright owner or owners.
- This written permission should be submitted with the proof-copy of the manuscript to be published in the Malaysian Journal of Science
Licensing Policy
Malaysian Journal of Science is an open-access journal that follows the Creative Commons Attribution-Non-commercial 4.0 International License (CC BY-NC 4.0)
CC BY – NC 4.0: Under this licence, the reusers to distribute, remix, alter, and build upon the content in any media or format for non-commercial purposes only, as long as proper acknowledgement is given to the authors of the original work. Please take the time to read the whole licence agreement (https://creativecommons.org/licenses/by-nc/4.0/legalcode ).
References
Berry, M. V. (1977). Semi-classical mechanics in phase space: a study of Wigner’s function. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 287(1343), 237-271.
Bizarro J. P. (1994). Weyl-Wigner formalism for rotation-angle and angular-momentum variables in quantum mechanics, Physical Review A, 49(5):3255.
Busch P., Grabowski M., Lahti P. J. (1997). Operational quantum physics (Vol. 31). Springer Science & Business Media.
Das A. (2020). Lectures on quantum field theory. World Scientific.
Dirac P. A. M. (1981). The principles of quantum mechanics (No. 27). Oxford University Press.
Hall B. C. (2013). Quantum theory for mathematicians. Springer.
Isham C. J. (1984). Topological and global aspects of quantum theory. In Relativity, groups and topology. 2. edited by B. S. Dewitt and R. Stora, North-Holland: Amsterdam, 1984, pp. 1059- 1290.
Iwai T. (1982). The symmetry group of the harmonic oscillator and its reduction. Journal of Mathematical Physics, 23(6):1088-1092.
Sundermeyer K. (1982). Constrained dynamics with applications to Yang-Mills theory, general relativity, classical spin, dual string model. New York, USA: Springer-Verlag.
Weinbub, J., & Ferry, D. K. (2018). Recent advances in Wigner function approaches. Applied Physics Reviews, 5(4).
Woit, P., Woit, & Bartolini. (2017). Quantum theory, groups, and representations. New York, NY, USA: Springer International Publishing.
Yamada K. (1982). Angular-momentum—angle commutation relations and minimum-uncertainty states. Physical Review D, 25(12):3256.
Zhang, K. Y., & Feng, W. Z. (2023). Explaining the W boson mass anomaly and dark matter with a U (1) dark sector. Chinese Physics C, 47(2), 023107.