MATHEMATICAL MODEL OF NICKEL-GRAPHENE COMPOSITE INKS FOR JETTING PROPERTIES IN INKJET PRINTING
Main Article Content
Abstract
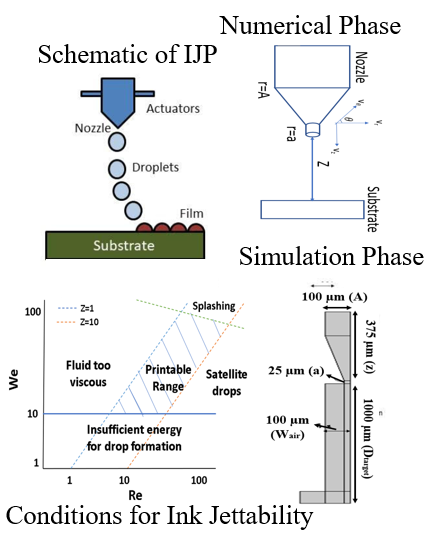
The droplet formation process in inkjet printing is studied numerically and verified through a simulation model. The droplet formation process decides the printing quality of the coating, and a mathematical model is developed to understand the complete process from droplet formation to detachment. The Navier-Stokes equation is used to mathematically derive the droplet radius (rnumerical). COMSOL multiphysics is used for simulation and the radius (rsimulation) is calculated from the droplet mass. The rnumerical and rsimulation are compared for inks containing nickel, graphene, and nickel-graphene composite ink it is observed that the composite ink radiuses have the lowest difference (rsimulation - rnumerical =0.085µm). A droplet is formed at 1.47mm from the nozzle inlet, for nickel-graphene ink, and after 1.5mm for other pristine inks. The results are verified through Z number, velocity profile, and droplet mass. The droplet formation observed from the velocity profile is earliest at 120µs. It is seen that a stable droplet is generated at 100µs for nickel-graphene ink and at 200 µs for individual inks.
Downloads
Article Details
Transfer of Copyrights
- In the event of publication of the manuscript entitled [INSERT MANUSCRIPT TITLE AND REF NO.] in the Malaysian Journal of Science, I hereby transfer copyrights of the manuscript title, abstract and contents to the Malaysian Journal of Science and the Faculty of Science, University of Malaya (as the publisher) for the full legal term of copyright and any renewals thereof throughout the world in any format, and any media for communication.
Conditions of Publication
- I hereby state that this manuscript to be published is an original work, unpublished in any form prior and I have obtained the necessary permission for the reproduction (or am the owner) of any images, illustrations, tables, charts, figures, maps, photographs and other visual materials of whom the copyrights is owned by a third party.
- This manuscript contains no statements that are contradictory to the relevant local and international laws or that infringes on the rights of others.
- I agree to indemnify the Malaysian Journal of Science and the Faculty of Science, University of Malaya (as the publisher) in the event of any claims that arise in regards to the above conditions and assume full liability on the published manuscript.
Reviewer’s Responsibilities
- Reviewers must treat the manuscripts received for reviewing process as confidential. It must not be shown or discussed with others without the authorization from the editor of MJS.
- Reviewers assigned must not have conflicts of interest with respect to the original work, the authors of the article or the research funding.
- Reviewers should judge or evaluate the manuscripts objective as possible. The feedback from the reviewers should be express clearly with supporting arguments.
- If the assigned reviewer considers themselves not able to complete the review of the manuscript, they must communicate with the editor, so that the manuscript could be sent to another suitable reviewer.
Copyright: Rights of the Author(s)
- Effective 2007, it will become the policy of the Malaysian Journal of Science (published by the Faculty of Science, University of Malaya) to obtain copyrights of all manuscripts published. This is to facilitate:
- Protection against copyright infringement of the manuscript through copyright breaches or piracy.
- Timely handling of reproduction requests from authorized third parties that are addressed directly to the Faculty of Science, University of Malaya.
- As the author, you may publish the fore-mentioned manuscript, whole or any part thereof, provided acknowledgement regarding copyright notice and reference to first publication in the Malaysian Journal of Science and Faculty of Science, University of Malaya (as the publishers) are given. You may produce copies of your manuscript, whole or any part thereof, for teaching purposes or to be provided, on individual basis, to fellow researchers.
- You may include the fore-mentioned manuscript, whole or any part thereof, electronically on a secure network at your affiliated institution, provided acknowledgement regarding copyright notice and reference to first publication in the Malaysian Journal of Science and Faculty of Science, University of Malaya (as the publishers) are given.
- You may include the fore-mentioned manuscript, whole or any part thereof, on the World Wide Web, provided acknowledgement regarding copyright notice and reference to first publication in the Malaysian Journal of Science and Faculty of Science, University of Malaya (as the publishers) are given.
- In the event that your manuscript, whole or any part thereof, has been requested to be reproduced, for any purpose or in any form approved by the Malaysian Journal of Science and Faculty of Science, University of Malaya (as the publishers), you will be informed. It is requested that any changes to your contact details (especially e-mail addresses) are made known.
Copyright: Role and responsibility of the Author(s)
- In the event of the manuscript to be published in the Malaysian Journal of Science contains materials copyrighted to others prior, it is the responsibility of current author(s) to obtain written permission from the copyright owner or owners.
- This written permission should be submitted with the proof-copy of the manuscript to be published in the Malaysian Journal of Science
Licensing Policy
Malaysian Journal of Science is an open-access journal that follows the Creative Commons Attribution-Non-commercial 4.0 International License (CC BY-NC 4.0)
CC BY – NC 4.0: Under this licence, the reusers to distribute, remix, alter, and build upon the content in any media or format for non-commercial purposes only, as long as proper acknowledgement is given to the authors of the original work. Please take the time to read the whole licence agreement (https://creativecommons.org/licenses/by-nc/4.0/legalcode ).
References
Altay BN, Jourdan JS, Turkani VS, et al. (2018) Fundamental Mechanism of Ink Film Roughness The Impact of Substrate and Process on the Electrical Performance of Screen-Printed Nickel Electrodes. ACS Appl. Energy Mater. 1: 7164-7173
Burlington M. (2018) CFD Module User’s Guide; COMSOL.
Chen H, Zhang Y, Ma Y, et al. (2020) Sand-Milling Exfoliation of Structure Controllable Graphene for Formulation of Highly Conductive and Multifunctional Graphene Inks. 12: 56319-56329
Cherne FJ, Baskes MI, Deymier PA. (2002) Properties of liquid nickel: A critical comparison of EAM and MEAM calculations. Phys Rev B - Condens Matter Mater Phys. 65.
Derby B. (2015) 3D Printing — Review Additive Manufacture of Ceramics Components by Inkjet Printing. Engineering. 1:113-123.
Farraj Y, Grouchko M, Magdassi S, Koch F., Wittkotter M., Muller M., Reinhold I., Zapka W. (2014). Ink-jet printed copper complex MOD ink for plastic electronics, International Conference on Digital Printing Technologies. 51: 1587-1590
Gao Y, Shi W, Wang W, Leng Y, Zhao Y. (2014) Inkjet printing patterns of highly conductive pristine graphene on flexible substrates. Ind Eng Chem Res. 53: 16777-16784.
Hoath S. D. (2016) Fundamentals of Inkjet Printing: The Science of Inkjet and Droplets. (Hoboken, ed.). John Wiley & Sons.
Kulkarni VS., Shaw C. (2016). Surfactants, Lipids, and Surface Chemistry. Essent Chem Formul Semisolid Liq Dosages
Li D (2001) Interface Science and Technology.
Murthy H., Thakur N., and NS. (2022). Nickel-Based Inks for Flexible Electronics - A Review on Recent Trends. Journal of Adv Manuf Syst. 21: 591-624.
Ramachandran H, Jahanara MM, Nair NM, Swaminathan P. (2020) Metal oxide heterojunctions using a printable nickel oxide ink. RSC Adv. 10: 3951-3959
Rev. BS. (2018) On the development of the Navier–Stokes equation byNavier. Hist Phys Relat Sci. 40: 1-12.
Rudyak V. Ya., Belkin (2011) A. A. Egorov V. V. IDA. Simulation of flows in nanochannels by the molecular dynamics method. Nanosyst Physics, Chem Math. 2:100-112.
Secor EB, Ahn BY, Gao TZ, Lewis JA, Hersam MC. (2015) Rapid and Versatile Photonic Annealing of Graphene Inks for Flexible Printed Electronics. Adv Mater. 27
Takuya O., Tsubouchi S., and Suwa Y. (2023). Analysis of the Ink-stream Break-Up Phenomenon in Continuous Inkjet Printing. ACS Omega. 8: 34442-34447.
Thakur N, Murthy H. (2021) Nickel-Based Inks for Inkjet Printing : A Review on Latest Trends. 11: 20-35.
Tofan T., Borodinas S., Kacianauskas R., and Jasevicius R. (2022). Modeling 3D Droplet Movement Using a Drop-on-Demand Inkjet Printhead Model. Processes MDPI: 10, 147.
Tofan Tim, Kruggel Emdem Harald, Turla Vytautas JR. (2021) Numerical Modeling of the Motion and Interaction of a Droplet of an Inkjet Printing Process with a Flat Surface. Appl Sci. 11: 527.